Programmation Fonctionnelle Avancée

Cours 12

kn@lmf.cnrs.fr
https://usr.lmf.cnrs.fr/~kn

Préparation aux évaluations

On donne quelques exemples d'exercices :

Il permettent d'aborder tous les points du cours
Ils illustrent le niveau de difficutlé attendu
Ce ne sont pas des modèles, les exercices demandés en examen/TP seront différents (i.e. il ne s'agit pas de changer les valeurs)

Il faut donc comprendre la façon de résoudre les problèmes, pas essayer de « copier/coller » le code du corrigé

Ce qui ne peut pas être corrigé aujourd'hui sera mis en ligne après le cours.

TP notés: aide-mémoire + cours + corrigés de TP disponible, notes manuscrites autorisées

Examen: aide-mémoire fourni dans le sujet, notes manuscrites et personnelles autorisées

Les notes sont manuscrites et personnelles. Exception : étudiants qui composent sur ordinateur peuvent avoir des notes tapées et imprimées.

Rappels OCaml (1)

(2 points) Écrire une fonction


  val compress : int list -> (int * int) list

Qui prend en argument une liste d'entiers triés par ordre croissant et qui renvoie une liste de paires (v, n) où v est un entier de la liste originale et n le nombre de fois où l'entier est répété.


let () = 
  assert ((compress [ 1;1;1;2;2;10;12;12;12 ]) = [1,3; 2,2; 10,1; 12,3]);
  assert ((compress [ 2;3;4 ]) = [2,1; 3,1; 4,1]);
  assert ((compress [ ]) = [ ])

Rappels OCaml (2)

(2 points) Écrire une fonction


  val find_last_map : ('a -> 'b option) -> 'a list -> 'b option

Qui prend en argument une fonction f, une liste l et renvoie le dernier élément de la liste l pour lequel f renvoie une valeur différente de None. Si aucun élément n'est trouvé, la fonction renvoie None. La fonction doit être récursive terminale.


  let f n = if n > 10 then Some (string_of_int n) else None

  let () =
    assert ((find_last_map f [100; 2; 200]) = Some "200");
    assert ((find_last_map f []) = None);
    assert ((find_last_map f [1;2;3]) = None)

Arbres binaires de recherche (1)

On suppose que l'on est dans un foncteur Make permettant de construire un ensemble en prenant en argument un module définissant un type de valeurs et une fonction de comparaison.


module type COMPARABLE =
sig
  type t
  val compare : t -> t -> int
end
module Make (E : COMPARABLE) =
struct
  (* Arbres équilibrés de type AVL *)
  type t = Nil  (* arbre vide *)
        | Node of (int, t, E.t, t) (* hauteur, gauche, element, droite *)

  let empty = Nil
  (** [merge t1 t2] renvoie l'union de [t1] et [t2] sous 
      forme d'un arbre équilibré *)
  let merge t1 t2 = ... 
 end

Arbres binaires de recherche (2)

Donner le code des fonctions suivantes, supposées écrites dans le foncteur. Les fonctions demandées qui produisent un arbre doivent produire un arbre équilibré. Lorsque l'on parle d'ordre, d'égalité de comparaison, on sous-entend toujours, « selon la fonction de comparaison du module E».

(0.5 point) val singleton : E.t -> t renvoie l'arbre contenant une valeur
(1 point) val add : E.t -> t ->t ajoute un élément à un arbre donné
(1.5 point) val mem : E.t -> t -> bool teste si un élément est dans l'arbre
(2 points) val inter : t -> t -> t renvoie l'intersection des deux ensembles
(2 points) val range : E.t -> E.t -> t -> E.t list telle que range e1 e2 t renvoie la liste des valeurs de t comprises entre e1 et e2 inclus. La liste renvoyée doit être ordonnée par valeurs croissantes.

Arbres binaires de recherche/foncteurs (3)

On suppose maintenant que l'on est à l'extérieur du foncteur, vous pouvez utiliser toutes les fonctions décrites dans le slide précédant mais pas « merge ». Vous ne pouvez utiliser les fonctions de comparaisons d'OCaml (compare, <,...) que sur le type int.

(2 points) Définir un module Date : COMPARABLE qui représente des dates comme des triplets d'entiers (année, jour, mois)
(1 point) Appliquer le foncteur Set.Make pour obtenir une implémentation d'un ensemble de dates dans un module appelé DateSet dans la suite.
(1 point) On suppose qu'un calendrier est un ensemble de dates. Donner une fonction: val creneaux_reunion : DateSet.t -> DateSet.t -> Date.t -> Date.t -> unit qui affiche dans la console sous la forme "jour/moi/année" la liste des créneaux se trouvant après la première date, avant la seconde date (inclus) et compatible avec les deux calendriers.

Types mutables, tables de hachage. (1)

On se donne une grille, représentée par un tableau de chaînes de caractères.


[|  ".....*...5..";
    "..4.5.....2*";
    "...*......*.";
    ".....7......"; |]

(4 points) Les caractères sont uniquement « . », « * » ou un chiffre. On souhaite compter le nombre de chiffres possédant une étoile dans une case adjacente, c'est à dire, juste au dessus, à droite, à gauche, en dessous ou dans les diagonales:


 ... 
 .5.
 ...

Dans la grille d'exemple, la réponse est 3 (le 4, 5, 2 de la deuxième ligne vérifient la condition).

Indication faire une fonction auxiliaire pour tester les cases autour d'une case donnée, et une fonction auxiliaire pour tester que des coordonnées sont valides.

Types mutables, tables de hachage. (2)

On considère la définition ci-dessous.


let f =
    let cache = Hashtbl.create 16 in
    fun x -> ...

(1 point) Que contient l'identifiant f une fois sa définition évaluée
(3 points) On suppose une fonction val get_http_ressource : string -> string qui prend en argument une chaîne de caractères représentant une adresse internet du style https://www.universite-paris-saclay.fr/index.html et qui renvoie le contenu du fichier associé sous forme d'une chaîne.
Écrire une fonction get_http_ressource_cache : string -> string qui:
- Récupère la ressource demandée au moyen de get_http_ressource au premier appel de la fonction.
- Garde en cache le résultat et le renvoi pour les 10 prochains appels sur la même adresse
- Au 11ème redemande la ressource et la met de nouveau en cache pour 10 appels.

Trie

On rappelle la définition du type trie en OCaml (celle fonctionnant comme une ensemble de chaînes, utilisant simplement un booléen pour indiquer qu'un nœud est terminal).


type trie = Node of bool * (char * trie) list

(4 points) Écrire une fonction val after_prefix : trie -> string -> trie qui renvoie le trie de tous les mots « plus grands » que la chaîne donnée au sens de l'ordre du dictionnaire. Si le trie contient les mots { "AB", "ABCD", "ABCD", "ABCEF", "AC", "XYZ"} l'appel de la fonction sur la chaîne "ABCE" doit renvoyer le trie contenant : { "ABCEF", "AC", "XYZ"}

Retour arrière

On suppose qu'un graphe est représenté par le type OCaml suivant:


    type graph = (int, int list) Hashtbl.t

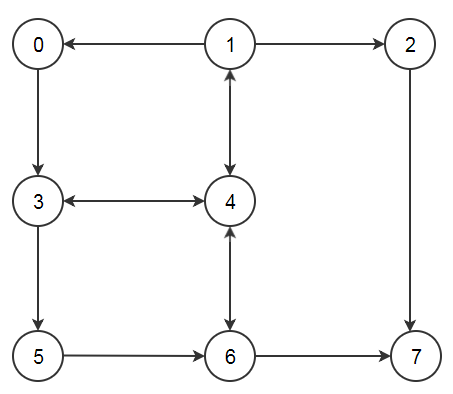
Les sommets du graphe sont des entiers entre 0 et n-1 où n est la taille de la table de hachage (le nombre de clés, donné par Hashtbl.length), associés à la liste des sommets voisin. Par exemple


let graph = Hashtbl.create 16
let () =
  Hashtbl.add graph 0 [3];
  Hashtbl.add graph 1 [0;2;4];
  Hashtbl.add graph 2 [7];
  Hashtbl.add graph 3 [4;5];
  Hashtbl.add graph 4 [1;3;6];
  Hashtbl.add graph 5 [6];
  Hashtbl.add graph 6 [4;7];
  Hashtbl.add graph 7 []

Retour arrière

(4 points) Donner une fonction circuit : (int list -> unit) -> graph ->unit prenant en argument une fonction f et appelant cette dernière sur tous les circuits Hamiltoniens, c'est à dire tous les chemins qui passent par l'ensemble des sommets du graphe une seule fois.
Pour le graphe précédent, [0;3;5;6;4;1;2;7] est une solution (la seule).

Conclusion

Cet ensemble de question est très long (31 points), ça ne sera pas aussi long
N'importe laquelle des catégorie (rappels, ABR, Mutables/Hachage/Trie/Backtracking) est au programme, ce sera un mélange.
Il n'y aura pas d'algorithmes « nouveaux », uniquement des variantes de de fonctions vues en TP ou dans ces supports.
Attention, variantes ne veut pas dire qu'il suffit copier/coller la solution sans comprendre…