Qu'est-ce qu'une fonction ?
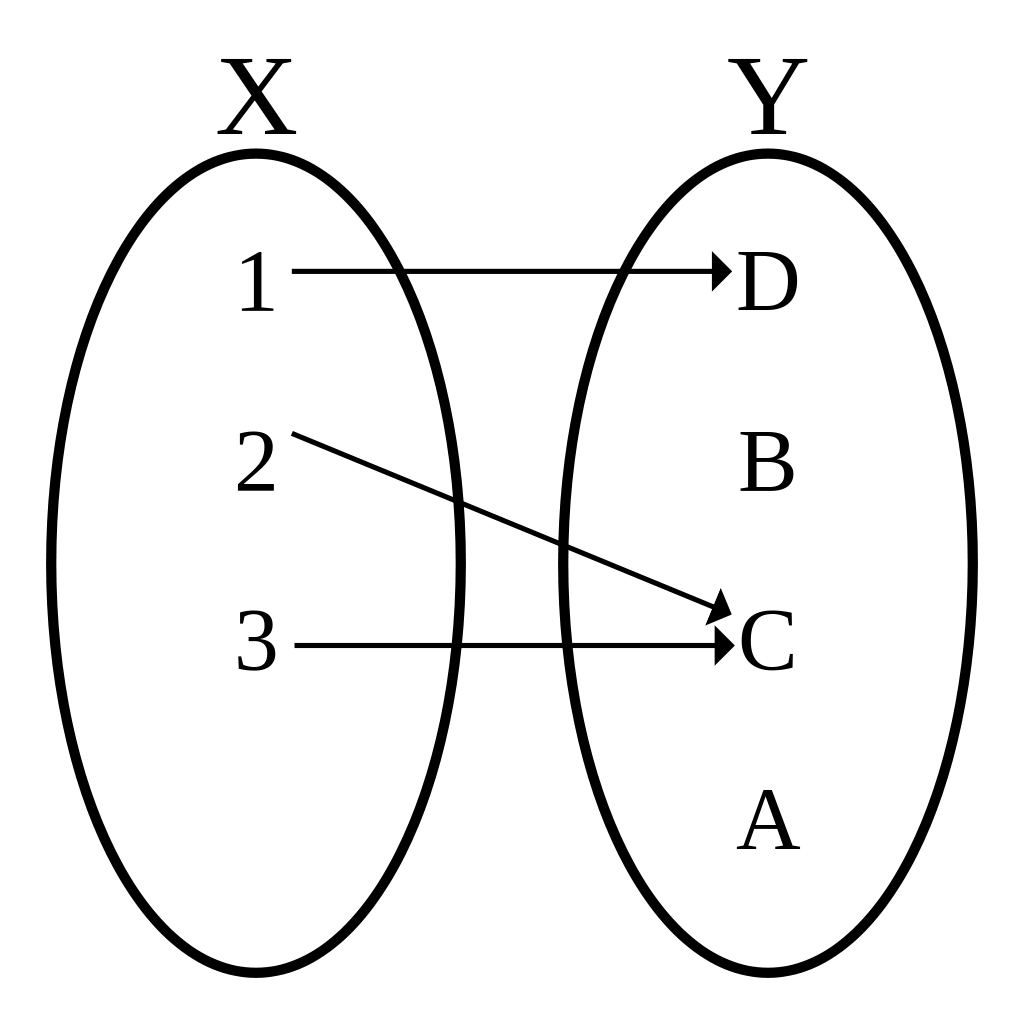
(mathématiques) c'est une relation binaire entre deux ensembles X et Y qui à tout élément de X associe un unique élément de Y.
(programmation) c'est un machin qui fait un truc.
(mathématiques) c'est une relation binaire entre deux ensembles X et Y qui à tout élément de X associe un unique élément de Y.

(programmation) c'est un machin qui fait un truc.
En mathématique le concepte de fonction :
Développement de la programmation :
Exemple en Python : on souhaite dessiner un damier rouge/bleu avec turtle dont les carrés font 20 pixels de large en partant de x=0, y=0, vers le haut, de 7 lignes de large et 7 lignes de hauteur.

from turtle import *
up() #on leve le crayon
for i in range(7):
#Les lignes paires commencent
#par un carré rouge, les lignes
#impaires par un carré bleu
if i % 2 == 0:
couleur = "red"
else:
couleur = "blue"
for j in range(7):
x=j*20
y=i*20
goto(x, y)
color(couleur)
down()
begin_fill()
goto(x+20, y)
goto(x+20, y+20)
goto(x, y+20)
goto(x,y)
end_fill()
up()
#Après chaque carré, on change
#la couleur
if couleur == "red":
couleur = "blue"
else:
couleur = "red"
#On a fini, on attend
done()
Supposons que l'on veuille faire plusieurs damiers dans notre programme, avec des caractéristiques différentes :
Si on fait un copier/collé :
C'est une très mauvaise pratique
En Python, le mot clé def premet de définir une fonction
def dessine_damier(x0, y0, c1, c2, l, h, t):
for i in range(h):
if i % 2 == 0:
couleur = c1
else:
couleur = c2
for j in range(l):
x=j*t + x0
y=i*t + y0
goto(x, y)
color(couleur)
down()
begin_fill()
goto(x+t, y)
goto(x+t, y+t)
goto(x, y+t)
goto(x,y)
end_fill()
up()
if couleur == c1:
couleur = c2
else:
couleur = c1
Une définition de fonction peut ensuite être réutilisée.
from turtle import *
def dessine_damier(x0, y0, c1, c2, l, h, t):
...
#on veut dessiner trois damiers différents :
dessine_damier(0,0, "red", "blue", 7, 7, 20)
dessine_damier(0,200, "yellow", "purple", 4, 4, 10)
dessine_damier(-200, 0, "black", "green", 5, 5, 30)
done()

Q : est-ce que la fonction dessine_damier est une fonction au sens mathématique du terme ?
Pas vraiment :
Non c'est plus compliqué que ça : toutes les chaînes ne sont pas valide, les entiers trop grands ne sont par représentable en Python (pas assez de mémoire), toutes les tailles de pixel ne sont pas valides, …
Non c'est plus compliqué que ça : la fonction ne renvoie rien, mais elle a un comportement différent selon les différentes valeurs de ces arguments,…
def f(x) :
return x ** 3 - 4 ** 2 + 1
tab = [0] * 100
for i in range(len(tab)):
tab[i] = f(i)
Ici la fonction Python f se comporte comme une fonction mathématique. Pour une valeur d'entrée elle renvoie un résultat.
En programmation, on a deux façons de calculer :
Ces concepts existent depuis le début de la programmation. Dans beaucoup de langages (par exemple Pascal), on avait une distinction :
Le langage Python, comme beaucoup de langages modernes, ne fait pas de distinction entre procédure et fonctions.
def nom_de_la_fonction(x1, x2, …, xn):
i1
i2
…
im
Dans une fonction, le mot clé return permet de
quiter la fonction. Si la fonction doit renvoyer un résultat,
alors on peut donner une expression en argument
à return qui calculera la valeur renvoyée.
En l'absence de return une fonction se termine
lorsque l'on arrive à la dernière instruction de son corps.
##renvoie l'inverse de x si x != 0 et 0 sinon
def inv_ou_0(x):
if x == 0:
return 0
else:
return 1/x
Attention, Python ne vérifie pas si une fonction possède bien un return dans tous les cas !
def inv_ou_0_bug(x):
if x != 0:
return 1/x
#On ne fait pas de return dans l'autre cas donc
#la fonction « ne renvoie rien »
>>> x = inv_ou_0_bug(2)
>>> y = inv_ou_0_bug(0)
>>> x+4
4.5
>>> y+4
Traceback (most recent call last):
File "", line 1, in <module>
TypeError: unsupported operand type(s) for +: 'NoneType' and 'int'
Il n'y a « rien » dans la variable y, donc l'opérateur + échoue (on précisera ça plus tard).
Si une fonction est définie avec n paramètres, alors il faut l'appeler avec exactement n arguments.
def f(x, y):
return x*x + y*y
>>> f(2,3)
13
>>> f(2)
Traceback (most recent call last):
File "", line 1, in <module>
TypeError: f() missing 1 required positional argument: 'y'
>>> f(2, 3, 4)
Traceback (most recent call last):
File "", line 1, in <module>
TypeError: f() takes 2 positional arguments but 3 were given
def f(x, y):
if x != y:
return x*x + y*y
else:
reutrn 0
f(4, 5)
On rappelle que dans l'architecture de Von Neumann, un ordinateur possède de la mémoire (pour stocker les résultats, les variables, …) et des registres (sur lequels le processeur peut effectuer des opérations)
On se donne un langage machine fictif pour une architecture comme celle de Von Neumann :
r0 # registre de travail
r1 # registre de travail
PC # registre contenant l'adresse de l'instruction en cours
SP # registre spécial
load ri n # charge l'entier n dans le registre ri
read rdst src # lit la valeur stockée à l'adresse
# source et stocke la stocke dans le registre rdst
# src peut etre une adresse ou un registre contenant une adresse
write rsrc dst # lit la valeur du registre rsrc
# et la stocke la stocke dans dst
# dst peut etre une adresse ou un registre contenant une adresse
add rd ra b # rd ← ra + b, b peut être un registre ou un entier
jump dst # saute à l'instruction dont l'adresse est dst.
jgt ra rb dst # saut à l'instruction dont l'adresse est dst si ra > rb
On considère le petit programme Python ci-dessous :
x = 42
if x > 13:
y = 31
else:
y = 32
Traduit dans le langage machine fictif :
load r0 42 #charge la constante 42 dans le registre r0
write r0 0x0f40 #copie le contenu de r0 à l'adresse 0x0f40 (x)
read r0 0x0f40 #copie le contenu de l'adresse 0x0f40 dans r0
load r1 13 #charge la constante 13 dans le registre r1
jgt r0 r1 0x0270 #si r0 > r1, saute à l'adresse 0x0232
load r0 32 #charge 32 dans r0
write r0 0x0f18 #copie le contenue de r0 à l'adresse 0x0f18 (y)
jump 0x0280 #saute à l'adresse
load r0 31 #charge 31 dans r0
write r0 0x0f18 #copie le contenue de r0 à l'adresse 0x0f18 (y)
adresse valeur (registres) r0 : 4231 r1 : 13
0x0230
load r0 42
◀
segment de code :
La partie de la mémoire qui contient
les instructions machines
0x0238
write r0 0x0f40
◀
0x0240
read r0 0x0f40
◀
0x0248
load r1 13
◀
0x0250
jgt r0 r1 0x0270
◀
0x0258
load r0 32
0x0260
write r0 0x0f18
0x0268
jump 0x0280
0x0270
load r0 31
◀
0x0278
write r0 0x0f18
◀
◀
0x0f18 (y)
31
tas :
La partie de la mémoire qui contient les
données allouées par le programme
(entier, chaînes de caractères, tableaux, …)
0x0f40 (x)
42
Mais globalement c'est une bonne approximation de la réalité
On considère maintenant le programme suivant
def f(x, y):
return x + y
u = f(41, 42)
v = f(42, 43)
Plein de choses à prendre en compte
Solution : on utilise une troisième zone mémoire, la pile.
La pile est une structure de données hyper-super-mega importante en
informatique. Elle sera présentée en détail au S2 (« UE : algorithmique
et structures de données »).
La pile d'appel est une zone particulière de la mémoire et
manipulée par le processeur.
Un registre particulier, SP (stack pointer)
contient l'adresse du sommet de la pile.
Pour appeler une fonction en langage machine :
Initialement, SP est une adresse très grande, que l'on va diminuer de 8 en 8 au fur et à mesure qu'on empile.
add SP SP -8 # on réserve de l'espace pour le résultat
write r0 SP # on sauvegarde r0 sur la pile
add SP SP -8
write r1 SP # on sauvegarde r1 sur la pile
add SP SP -8
load r0 41 # on charge 41 dans r0
write r0 SP # on écrit 41 sur la pile
add SP SP -8
load r0 42 # on charge 42 dans r0
write r0 SP # on écrit 42 sur la pile
add SP SP -8
write PC SP # on sauvegarde PC (l'endroit où on est) sur la pile
add SP SP -8
jump 0x300 # on saute à l'adresse de f
adresse valeur PC
0x0408
add SP SP -8
◀
0x0410
write r0 SP
◀
0x0418
add SP SP -8
◀
0x0420
write r1 SP
◀
0x0428
add SP SP -8
◀
0x0430
load r0 41
◀
0x0438
write r0 SP
◀
0x0440
add SP SP -8
◀
0x0448
load r0 42
◀
0x0450
write r0 SP
◀
0x0458
add SP SP -8
◀
0x0460
write PC SP
◀
0x0468
add SP SP -8
◀
0x0470
jump 0x300
◀
adresse valeur SP
tas
0x0f18
pile
0xefd0
◀
0xefd8 (@ret)
0x0460
◀
0xefe0 (y)
42
◀
0xefe8 (x)
41
◀
0xeff0
(valeur r1)
◀
0xeff8
(valeur r0)
◀
0xf000 (val. renv.)
◀
(registres) r0 : (valeur)4142 r1 : (valeur)
On est arrivé dans le code de la fonction f (à l'adresse 0x0300)
add r0 SP 24 # on lit SP+24 i.e. l'adresse de x dans r0
read r0 r0 # on charge ce qu'il y a à l'adresse r0 dans r0
add r1 SP 16 # on lit SP+16 i.e. l'adresse de y dans r1
read r1 r1 # on charge ce qu'il y a à l'adresse r1 dans r1
add r0 r0 r1 # on fait la somme de x + y
add r1 SP 48 # on calcule dans 41 l'adresse où écrire le résultat
write r0 r1 # on écrit r0 à l'adresse contenue dans r1
add SP SP 8
read r0 SP # on lit l'adresse de retour dans r0
add r0 r0 24 # on se position sur la bonne instruction
jump r0 # on saute à l'adresse r0, i.e. là où on doit revenir
adresse valeur PC
0x0300
add r0 SP 24
◀
0x0308
read r0 r0
◀
0x0310
add r1 SP 16
◀
0x0318
read r1 r1
◀
0x0320
add r0 r0 r1
◀
0x0328
add r1 SP 48
◀
0x0330
write r0 r1
◀
0x0338
add SP SP 8
◀
0x0340
read r0 SP
◀
0x0348
add r0 r0 24
◀
0x0350
jump r0
◀
adresse valeur SP
tas
0x0f18
0xefd0
◀
pile
0xefd8 (@ret.)
0x0460
◀
0xefe0 (y)
42
0xefe8 (x)
41
0xeff0
(valeur r1)
0xeff8
(valeur r0)
0xf000 (val. renv.)
83
(registres) r0 : 420xefe841830x04600x0478 r1 : (valeur)0xefe0420xf000
Quand on revient dans l'appelant, il faut nettoyer la pile :
add SP SP 24 # on saute les arguments
read r1 SP # on restore r1 à son ancienne valeur
add SP SP 8
read r0 SP # on restore r0 à son ancienne valeur
add SP SP 8
read r0 SP # on lit le résultat, i.e. f(41,42) dans r0
add SP SP 8
write r0 0xf18 # on écrit le résultat à l'adresse de u
adresse valeur PC
0x0470
jump 0x300
0x0478
add SP SP 24
◀
0x0480
read r1 SP
◀
0x0488
add SP SP 8
◀
0x0490
read r0 SP
◀
0x0498
add SP SP 8
◀
0x04a0
read r0 SP
◀
0x04a8
add SP SP 8
◀
0x04b0
write r0 0x0f18
◀
0x04b8
◀
adresse valeur SP
tas
0x0f18 (u)
83
pile
0xefd0
0xefd8
0x0460
◀
0xefe0
42
0xefe8
41
0xeff0
(valeur r1)
◀
0xeff8
(valeur r0)
◀
0xf000
83
◀
◀
(registres) r0 : 0x0478(valeur)83r1 : 0xf000(valeur)
La notion de pile d'appel, sur laquelle sont stockés :
Cette notion de pile permet d'appeler des fonctions dans des fonctions :
def h(x):
return x + 1
def g(x):
z = h(x+3) #point 3
return z
def f(x,y):
u = g(x) #point 2
return u + y
r = f(41, 42) #point 1
adresse valeur SP
pile
@retour point 3
44
@retour point 2
41
@retour point 1
42
41
Revenons aux fonctions en Python
def sumproduct(a, b, c):
tmp = a + b
tmp2 = tmp * c
return tmp2
Les variables tmp et tmp2 sont des variables locales à la fonction
Une variable définie en dehors d'une fonction est une variable globale
NOMBRE_UN = 1
def suivant(x):
return x + NOMBRE_UN
print(suivant(1)) # affiche 2
NOMBRE_UN = 17
print(suivant(1)) # affiche 18
Attention :
NOMBRE = 42
def change():
NOMBRE = 666
print ("Dans la fonction", NOMBRE)
return
change() #affiche Dans la fonction 666
print ("Hors de la fonction", NOMBRE) #affiche Hors de la fonction 42
Lorsque l'on écrit x = e dans une fonction (i.e. si x=e apparaît n'importe où dans la fonction)
Lorsque l'on utilise une variable x dans une fonction
X = 1
Y = 2
def f1(a, b):
X = a #X est locale
Y = b #Y est locale
def f2(a, b):
global X, Y
X = a #X global modifié
Y = b #Y global modifié
def f3():
return X+Y #pas de variable
#locale, va chercher
#les globales
def f4(a):
X = X + a
#erreur ! X = ... indique que le
#X est local pour toute la fonction.
#mais en faisant X + a
#X n'est pas défini !
return X
def f5():
print (X)
#erreur X est une variable locale
#(pas encore définie)
if False:
X = 42
Python, fait du passage par valeur des arguments aux fonctions. Cela signifie que les arguments sont copiés (sur la pile). Si une fonction modifie ses arguments, les modifications sont locales à la fonction.
def f(a):
a = 42
print(a)
a = 18
f(a) #affiche 42
print(a) #affiche 18
Dans une fonction, les paramètres se comportent comme des variables locales
Python fait du passage par valeur, mais la valeur d'un tableau est son adresse en mémoire.ATTENTION : c'est une différence fondamentale avec C++
def f(tab):
tab[0] = 42
tab = [1,2,3]
f(tab)
print(tab) #affiche [42, 2, 3]
On peut donc modifier les cases du tableau, mais pas la variable contenant le tableau:
def f(tab):
tab = "toto"
tab = [1,2,3]
f(tab)
print(tab) #affiche [1, 2, 3]