TD 5 - Construction d'automates déterministes à partir d'expressions régulières

Dans ce TD, on étudie une méthode de construction directe d'un automate fini déterministe à partir d'une expression régulière. Il s'agit d'un algorithme efficace, utilisé notamment dans ocamllex.

L'idée de départ est la suivante : si un automate fini reconnaît le langage correspondant à l'expression régulière r, alors à toute lettre d'un mot reconnu on peut faire correspondre une occurrence d'une lettre apparaissant dans r. Pour distinguer les différentes occurrences d'une même lettre dans r, on va les indexer par des entiers. Considérons par exemple l'expression régulière (a|b)* a (a|b), qui définit les mots sur l'alphabet {a,b} dont l'avant-dernière lettre est un a. Si on indice les caractères, on obtient

(a₁|b₁)* a₂ (a₃|b₂)

Si on considère le mot aabaab, alors il correspond à l'expression régulière de la manière suivante

a₁a₁b₁a₁a₂b₂

L'idée est alors de construire un automate dont les états sont des ensembles de lettres indexées, correspondant aux occurrences qui peuvent être lues à un instant. Ainsi l'état initial contient les premières lettres possibles des mots reconnus. Dans notre exemple, il s'agit de a₁,b₁,a₂. Pour construire les transitions, il suffit de calculer, pour chaque occurrence d'une lettre, l'ensemble des occurrences qui peuvent la suivre. Dans notre exemple, si on vient de lire a₁, alors les caractères possibles suivants sont a₁,b₁,a₂ ; si on vient de lire a₂, alors ce sont a₃,b₂.

Question 1. Nullité d'une expression régulière

On considère le type Caml suivant pour les expressions régulières dont les lettres sont indexées par des entiers (type ichar).

type ichar = char * int

type regexp =
  | Epsilon
  | Character of ichar
  | Union of regexp * regexp
  | Concat of regexp * regexp
  | Star of regexp

Écrire une fonction

val null : regexp -> bool

qui détermine si epsilon (le mot vide) appartient au langage reconnu par une expression régulière.

Question 2. Les premiers et les derniers

Pour représenter les ensembles de lettres indexées, on se donne le type Caml suivant :

module Cset = Set.Make(struct type t = ichar let compare = compare end)

Écrire une fonction

val first : regexp -> Cset.t

qui calcule l'ensemble des premières lettres des mots reconnus par une expression régulière. (Il faut se servir de null.)

De même, écrire une fonction

val last : regexp -> Cset.t

qui calcule l'ensemble des dernières lettres des mots reconnus.

Question 3. Les suivants

En se servant des fonctions first et last, écrire une fonction

val follow : ichar -> regexp -> Cset.t

qui calcule l'ensemble des lettres qui peuvent suivre une lettre donnée dans l'ensemble des mots reconnus.

On notera que la lettre d appartient à l'ensemble follow c r si et seulement si

soit il existe une sous-expression de r de la forme r₁r₂ avec d élément de first r₂ et c élément de last r₁ ;
soit il existe une sous-expression de r de la forme r₁* avec d élément de first r₁ et c élément de last r₁.

Question 4. Construction de l'automate

Pour construire l'automate déterministe correspondant à une expression régulière r, on procède ainsi :

on ajoute un nouveau caractère # à la fin de r ;
l'état de départ est l'ensemble first r ;
on a une transition de l'état q vers l'état q' à la lecture du caractère c (il s'agit là d'une lettre non indexée) si q' est l'union de tous les follow ci r pour tous les éléments ci de q tels que fst ci = c ;
les états d'acceptation sont ceux qui contiennent le caractère #.

Écrire une fonction

val next_state : regexp -> Cset.t -> char -> Cset.t

qui calcule l'état résultant d'une transition.

Pour représenter l'automate fini, on se donne le type Caml suivant :

module Cmap = Map.Make(Char)
module Smap = Map.Make(Cset)

type state = Cset.t

type autom = {
  start : state;
  trans : state Cmap.t Smap.t
}

On peut choisir de représenter ainsi le caractère # :

let eof = ('#', -1)

Écrire une fonction

val make_dfa : regexp -> autom

qui construit l'automate correspondant à une expression régulière. L'idée est de construire les états par nécessité, en partant de l'état initial. On pourra par exemple adopter l'approche suivante :

let make_dfa r =
  let r = Concat (r, Character eof) in
  (* transitions en cours de construction *)
  let trans = ref Smap.empty in
  let rec transitions q =
    (* la fonction transitions construit toutes les transitions de l'état q,
       si c'est la première fois que q est visité *)
    ...
  in
  let q0 = first r in
  transitions q0;
  { start = q0; trans = !trans }

Note : il est bien entendu possible de construire au final un automate dont les états ne sont pas des ensembles mais, par exemple, des entiers, pour plus d'efficacité dans l'exécution de l'automate. Cela pourrait d'ailleurs être fait pendant la construction, ou a posteriori. Mais ce n'est pas ce qui nous intéresse ici.

Visualisation avec l'outil dot

Voici du code pour imprimer un automate dans le format d'entrée de l'outil dot :

let fprint_state fmt q =
  Cset.iter (fun (c,i) ->
    if c = '#' then Format.fprintf fmt "# " else Format.fprintf fmt "%c%i " c i) q

let fprint_transition fmt q c q' =
  Format.fprintf fmt "\"%a\" -> \"%a\" [label=\"%c\"];@\n"
    fprint_state q
    fprint_state q'
    c

let fprint_autom fmt a =
  Format.fprintf fmt "digraph A {@\n";
  Format.fprintf fmt "  @[\"%a\" [ shape = \"rect\"];@\n" fprint_state a.start;
  Smap.iter
    (fun q t -> Cmap.iter (fun c q' -> fprint_transition fmt q c q') t)
    a.trans;
  Format.fprintf fmt "@]@\n}@."

let save_autom file a =
  let ch = open_out file in
  Format.fprintf (Format.formatter_of_out_channel ch) "%a" fprint_autom a;
  close_out ch

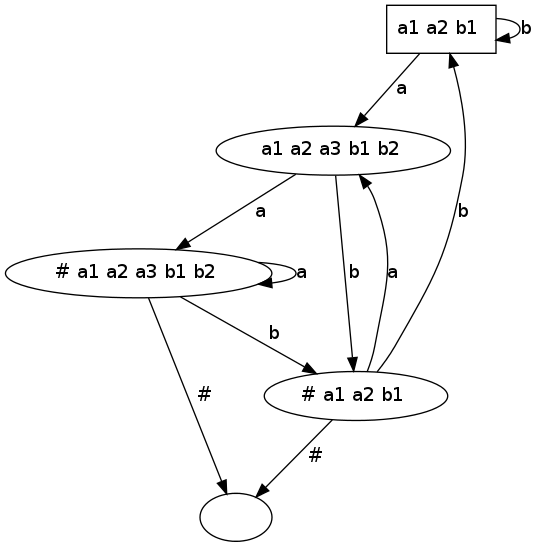Pour tester, on reprend l'exemple ci-dessus :

(*  (a|b)*a(a|b)  *)
let r = Concat (Star (Union (Character ('a', 1), Character ('b', 1))),
		Concat (Character ('a', 2),
			Union (Character ('a', 3), Character ('b', 2))))
let a = make_dfa r
let () = save_autom "autom.dot" a

L'exécution produit un fichier autom.dot qui peut être ensuite visualisé avec la commande Unix

  dotty autom.dot

ou encore avec la commande

  dot -Tps autom.dot | gv -

On doit obtenir quelque chose comme la figure de droite.

Question 5. Reconnaissance d'un mot

Écrire une fonction

val recognize : autom -> string -> bool

qui détermine si un mot est reconnu par un automate.

Voici quelques tests positifs :

let () = assert (recognize a "aa")
let () = assert (recognize a "ab")
let () = assert (recognize a "abababaab")
let () = assert (recognize a "babababab")
let () = assert (recognize a (String.make 1000 'b' ^ "ab"))

et quelques tests négatifs :

let () = assert (not (recognize a ""))
let () = assert (not (recognize a "a"))
let () = assert (not (recognize a "b"))
let () = assert (not (recognize a "ba"))
let () = assert (not (recognize a "aba"))
let () = assert (not (recognize a "abababaaba"))

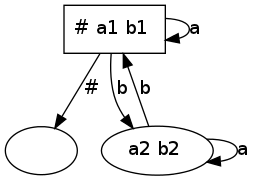
Voici un autre test avec une expression régulière caractérisant un nombre pair de b :

let r = Star (Union (Star (Character ('a', 1)),
		     Concat (Character ('b', 1),
			     Concat (Star (Character ('a',2)),
				     Character ('b', 2)))))
let a = make_dfa r
let () = save_autom "autom2.dot" a

Quelques tests positifs :

let () = assert (recognize a "")
let () = assert (recognize a "bb")
let () = assert (recognize a "aaa")
let () = assert (recognize a "aaabbaaababaaa")
let () = assert (recognize a "bbbbbbbbbbbbbb")
let () = assert (recognize a "bbbbabbbbabbbabbb")

et quelques tests négatifs :

let () = assert (not (recognize a "b"))
let () = assert (not (recognize a "ba"))
let () = assert (not (recognize a "ab"))
let () = assert (not (recognize a "aaabbaaaaabaaa"))
let () = assert (not (recognize a "bbbbbbbbbbbbb"))
let () = assert (not (recognize a "bbbbabbbbabbbabbbb"))

Question 6. Génération d'un analyseur lexical

Dans cette dernière question, on se propose de construire automatiquement, à partir de l'automate correspondant à une expression régulière, un code OCaml qui réalise une analyse lexicale, c'est-à-dire qui découpe une chaîne de caractères en lexèmes les plus longs possibles.

Plus précisément, on va produire un code de la forme suivante :

type buffer = { text: string; mutable current: int; mutable last: int }

let next_char b =
  if b.current = String.length b.text then raise End_of_file;
  let c = b.text.[b.current] in
  b.current <- b.current + 1;
  c

let rec state1 b =
  ...
and state2 b =
  ...
and state3 b =
  ...

Le type buffer contient la chaîne à analyser (champ text), la position du prochain caractère à examiner (champ current) et la position suivant le dernier lexème reconnu (champ last). La fonction next_char renvoie le prochain caractère à analyser et incrémente le champ current. Si la fin de la chaîne est atteinte, elle lève l'exception End_of_file.

À chaque état de l'automate correspond une fonction statei avec un argument b de type buffer. Cette fonction réalise le travail suivant :

Si l'état est acceptant, alors on affecte à b.last la valeur de b.current.
Puis on appelle next_char b et on examine son résultat. S'il s'agit d'un caractère pour lequel une transition existe, alors on appelle la fonction correspondante. Sinon, on lève une exception (par exemple, avec failwith "lexical error").

On note que les fonctions statei ne renvoient rien. Elles ne peuvent terminer que sur une exception (soit End_of_file pour signifier que la fin de la chaîne est atteinte, soit Failure pour signifier une erreur lexicale).

Écrire une fonction

  val generate: string -> autom -> unit

qui prend en arguments le nom d'un fichier et un automate et produit dans ce fichier le code OCaml correspondant à cet automate, selon la forme ci-dessus. Indications :

On pourra commencer par numéroter tous les états, par exemple en construisant un dictionnaire de type int Smap.t qui associe à chaque état un numéro unique.
On pourra s'inspirer du code de la fonction save_autom donnée plus haut pour ce qui est de l'affichage dans un fichier.

Note : Il sera utile d'ajouter au code produit une dernière ligne de la forme

  let start = state42

correspondant à l'état initial de l'automate.

Pour tester, écrire (dans un autre fichier lexer.ml, cette fois écrit à la main) un programme qui découpe une chaîne de caractères en lexèmes en utilisant le code produit automatiquement (en fixant le nom du fichier, par exemple a.ml). Le principe est une boucle qui effectue les actions suivantes :

on positionne le champ last à -1 ;
on appelle la fonction start et on rattrape l'exception e qu'elle lève ;
si le champ last vaut toujours -1, alors aucun lexème n'a été reconnu et on termine en relançant l'exception e ;
sinon, on affiche le lexème qui a été reconnu et on affecte au champ current la valeur du champ last.

Attention à traiter correctement l'arrêt du programme.

On pourra tester par exemple avec l'expression régulière (a|b)*b des mots qui se terminent par la lettre b, en exécutant

let r3 = Concat (Star (Character ('a', 1)), Character ('b', 1))
let a = make_dfa r3
let () = generate "a.ml" a

puis en liant le code produit avec le fichier lexer.m :

  % ocamlopt a.ml lexer.ml

Sur la chaîne abbaaab, l'analyse doit produire trois lexèmes et réussir :

--> "ab"
--> "b"
--> "aaab"

Sur la chaîne aba, l'analyse doit produire un premier lexème puis échouer :

--> "ab"
exception End_of_file

Enfin, sur la chaîne aac, l'analyse doit échouer sur une erreur lexicale :

exception Failure("lexical error")

On pourra aussi tester avec l'expression régulière (b|espilon)(ab)*(a|epsilon) des mots alternant les lettres a et b.

solution / lexer.ml

Cet algorithme est connu sous le nom d'algorithme de Berry-Sethi. Il est notamment décrit dans le dragon (Aho, Sethi, Ullman, Compilateurs), section 3.9.

retour à la page du cours