TD 1 - Mise à niveau Caml

Pour les TD, il est fortement conseillé de compiler le code OCaml (avec ocamlc ou ocamlopt), plutôt que d'utiliser le mode interactif d'OCaml (ocaml). Si vous travaillez sur un fichier file.ml vous le compilerez avec la commande ocamlopt -o file file.ml et l'exécuterez ensuite avec la commande ./file.

Vous êtes libres d'utiliser tout éditeur de texte de votre choix, à partir du moment où vous le maîtrisez et êtes à même de développer efficacement. Si vous souhaitez utiliser l'éditeur Emacs, voici quelques indications. On ouvre le fichier td1.ml en lançant la commande emacs td1.ml ou, si Emacs est déjà lancé, avec la commande Ctrl-x Ctrl-f. Vous pouvez compiler directement depuis Emacs avec la commande Meta-x compile (Meta s'obtient avec la touche Alt ou Esc, au choix). Vous pouvez relancer la même commande avec Meta-x recompile. Si le compilateur OCaml signale une erreur, vous pouvez vous placer directement sur la position correspondante avec Meta-x next-error. Vous pouvez simplifier les raccourcis clavier de ces trois commandes en insérant les lignes suivantes dans votre fichier ~/.emacs : 

(global-set-key [f5] 'compile)
(global-set-key [f6] 'recompile)
(global-set-key [f7] 'next-error)
C'est là une façon très efficace de travailler. (Et vous pourrez utiliser ces raccourcis pour toute autre chose que la programmation OCaml.)

Note : Pour ceux qui souhaitent travailler sous Windows, voici quelques indications pour utiliser OCaml sous Windows.

Ce TD comporte trois exercices indépendants. Ceux d'entre vous qui se sentent à l'aise avec Caml mais souhaitent tout de même faire l'exercice 1 sur les tris peuvent attaquer directement à la question tri par tas.

1. Tri

Dans ce premier exercice, nous allons programmer quelques tris classiques, sous la forme de fonctions opérant sur des listes d'entiers, c'est-à-dire ayant le type int list -> int list.

Tri par insertion

Écrire une fonction insertion : int -> int list -> int list qui insère un élément dans une liste d'entiers supposée triée en ordre croissant.

Écrire une fonction insertion_sort : int list -> int list qui réalise le tri par insertion d'une liste d'entiers. On rappelle que cela consiste à extraire le premier élément de la liste, à trier récursivement le reste de la liste, puis à insérer l'élément isolé (avec la fonction insertion).

On pourra tester avec le code suivant : 

let rec print fmt = function
 | [] -> ()
 | [x] -> Format.fprintf fmt "%d" x
 | x :: l -> Format.fprintf fmt "%d, %a" x print l

let rec is_sorted = function
 | [] | [_] -> true
 | x :: (y :: _ as l) -> x <= y && is_sorted l

let check l =
 let r = insertion_sort l in
 let ok = is_sorted r in
 Format.printf "[%a] => [%a]: %s@."
   print l print r (if ok then "OK" else "FAILED");
 if not ok then exit 1

let () =
 check [1; 2; 3];
 check [3; 2; 1];
 check [];
 check [1];
 check [2; 1; 1]
solution

Tri fusion (mergesort)

Écrire une fonction split : int list -> int list * int list qui prend une liste d'entiers l en argument et la « coupe en deux » c'est-à-dire renvoie une paire de liste (l1,l2) telle que les éléments de l sont exactement ceux de l1 et de l2 et telle que les listes l1 et l2 aient une longueur ne différant au plus d'un.

Écrire une fonction fusion : int list -> int list -> int list qui prend en arguments deux listes supposées triées en ordre croissant et les fusionne en une unique liste triée.

En utilisant les deux fonctions précédentes, écrire une fonction mergesort : int list -> int list réalisant le tri fusion. On rappelle que le principe consiste à couper la liste en deux, à trier récursivement chacune des deux listes obtenues, puis à fusion les deux listes triées.

Tester comme pour le tri par insertion.

solution

Tri rapide (quicksort)

Écrire une fonction partition : int -> int list -> int list * int list qui prend en argument un entier x et une liste d'entiers l et renvoie une paire de listes (l1,l2) telle que l1 (resp. l2) contient les éléments de l plus petits (resp. plus grands) que x.

Écrire une fonction quicksort : int list -> int list réalisant le tri rapide (quicksort). On rappelle que le principe consiste à isoler un élément particulier de la liste (ici le premier), à partionner les éléments restants en utilisant la fonction partition ci-dessus, à trier récursivement les deux listes obtenues, et enfin à recoller les morceaux. Pour cette dernière étape on pourra utiliser la fonction de bibliothèque List.append qui effectue la concaténation de deux listes (elle se note également @ de manière infixe).

Tester.

solution

Tri par tas (heapsort)

Structure de tas

Un tas est un arbre binaire contenant des entiers en chacun de ses noeuds et dont chaque sous-arbre t vérifie la propriété suivante : l'entier à la racine de t est inférieur ou égal à tous les entiers contenus dans t. Voici un exemple de tas contenant les entiers 1, 2, 2, 4, 5 et 6 : 
           1
          / \
         2   5
	/ \
       4   2
            \
	     6

Le but de cette question est de réaliser les deux opérations élémentaires sur la structure de tas que sont l'insertion d'un nouvel élément et l'extraction du plus petit élément (c'est-à-dire la racine). On se donne le type heap suivant pour représenter les tas : 

type heap = Null | Fork of int * heap * heap
On commence par une opération plus complexe, merge : heap -> heap -> heap, qui réalise la fusion de deux tas a et b. Le principe est le suivant. Si a ou b est Null, le résultat est immédiat. Sinon, on compare la racine de a et celle de b ; supposons que la racine de a soit la plus petite (sinon, on échange les rôles de a et b). Le résultat est alors un tas dont la racine est celle de a, dont le sous-arbre gauche est le sous-arbre droit de a, et dont le sous-arbre droit est obtenu en fusionnant récursivement le sous-arbre gauche de a et l'arbre b. Écrire la fonction merge.

À l'aide de la fonction merge, écrire une fonction add : int -> heap -> heap qui insère un nouvel élément dans un tas. (On pourra se servir du tas Fork (x, Null, Null) qui contient uniquement x.)

De même, utiliser la fonction merge pour écrire une fonction extract_min : heap -> int * heap qui extrait le plus petit élément d'un tas (sa racine) et renvoie le tas constitué par tous les autres éléments. Lorsque le tas est vide, on pourra lever l'exception Empty_heap ainsi déclarée : 

exception Empty_heap

Note : ces tas s'appellent des skew heaps et sont à la fois persistants, élégants et très efficaces.

On pourra tester avec le code suivant : 

let rec print_heap fmt = function
  | Null -> Format.fprintf fmt "Null"
  | Fork (x, a, b) ->
      Format.fprintf fmt "Fork (@[%d,@ %a,@ %a@])"
        x print_heap a print_heap b

let rec is_heap_rec min = function
  | Null -> true
  | Fork (x, l, r) -> min <= x && is_heap_rec x l && is_heap_rec x r

let is_heap = is_heap_rec min_int

let check_heap h =
  let ok = is_heap h in
  Format.printf "%a: %s@."
    print_heap h (if ok then "OK" else "FAILED");
  if not ok then exit 1

let () =
  let h1 = add 2 (add 1 (add 3 Null)) in
  check_heap h1;
  let h2 = add 4 (add 0 (add 1 Null)) in
  check_heap h2;
  let h = merge h1 h2 in
  check_heap h;
  let m, h = extract_min h in
  assert (m = 0);
  check_heap h

Application au tri

Une fois la structure de tas donnée, il est aisé d'en déduire un algorithme de tri, appelé tri par tas.

Pour cela, commencer par écrire une fonction heap_of_list : int list -> heap qui construit un tas avec tous les éléments d'une liste.

Écrire ensuite la fonction inverse list_of_heap : heap -> int list qui construit une liste triée avec tous les éléments d'un tas.

Enfin, combiner les deux fonctions précédentes en une fonction heapsort : int list -> int list réalisant le tri par tas.

Tester comme pour les autres tris.

solution

Paramétricité

Les fonctions de tri précédentes utilisent la fonction de comparaison prédéfinie d'OCaml. On souhaite les généraliser afin qu'elles s'appliquent à des listes dont les éléments sont munis d'une relation d'ordre arbitraire.
  1. Une première solution consiste à utiliser l'ordre supérieur, pour passer la fonction de comparaison en argument. Reprendre le code de l'une des fonctions de tri ci-dessus et en faire une fonction de type 
      sort : ('a -> 'a -> bool) -> 'a list -> 'a list
    où la fonction passée en argument correspond à la relation « inférieur ou égal à ».

    On pourra tester ainsi : 

    let rec is_sorted le = function
  | [] | [_] -> true
  | x :: (y :: _ as l) -> le x y && is_sorted le l

let check le l =
  let r = sort le l in
  let ok = is_sorted le r in
  Format.printf "[%a] => [%a]: %s@."
    print l print r (if ok then "OK" else "FAILED");
  if not ok then exit 1

let () =
  check (<=) [1; 2; 3];
  check (<=) [3; 2; 1];
  check (<=) [];
  check (<=) [1];
  check (<=) [2; 1; 1];
  check (>=) [1; 2; 3];
  check (>=) [3; 2; 1];
  check (>=) [];
  check (>=) [1];
  check (>=) [2; 1; 1]
    solution
  2. Une autre solution consiste à écrire la fonction de tri à l'intérieur d'un foncteur, dont l'argument spécifie le type des éléments de la liste et la fonction de comparaison. Reprendre le code de l'une des fonctions de tri et en faire un foncteur de la forme 
      module Sort(X : sig type t val le : t -> t -> bool end) : sig
    val sort : X.t list -> X.t list
  end = struct
    let sort l =
      ...
  end
    On pourra tester avec des entiers, ainsi : 
    module S = Sort(struct type t = int let le = (<=) end);;

let rec print fmt = function
  | [] -> ()
  | [x] -> Format.fprintf fmt "%d" x
  | x :: l -> Format.fprintf fmt "%d, %a" x print l

let rec is_sorted le = function
  | [] | [_] -> true
  | x :: (y :: _ as l) -> le x y && is_sorted le l

let check l =
  let r = S.sort l in
  let ok = is_sorted (<=) r in
  Format.printf "[%a] => [%a]: %s@."
    print l print r (if ok then "OK" else "FAILED");
  if not ok then exit 1

let () =
  check [1; 2; 3];
  check [3; 2; 1];
  check [];
  check [1];
  check [2; 1; 1]
    solution

2. Le mode T9 des téléphones portables

Le mode T9 des téléphones portables facilite la saisie des textes sur les claviers : au lieu de taper plusieurs fois sur une touche pour faire défiler les lettres, une seule frappe suffit et le téléphone propose de lui-même les mots qui correspondent à la séquence de touches qui vient d'être tapée, à partir d'un dictionnaire qu'il a en mémoire.

Par exemple, en tapant successivement les touches 2, 6, 6, 5, 6, 8 et 7 vous obtenez le mot bonjour. Il est possible qu'une suite de touches corresponde à plusieurs mots. Ainsi, la suite 5, 6, 4 et 3 correspond aux mots joie et loge et la suite 2, 5, 3 et 3 à clef et bled.

Le but de cet exercice est de programmer une solution efficace pour la recherche des mots du dictionnaire qui correspondent à une séquence de touches. Pour cela, nous allons représenter le dictionnaire par un arbre digital (en anglais trie) c'est-à-dire un arbre où chaque branche est étiquetée par le numéro d'une touche du téléphone et chaque noeud par les mots du dictionnaire correspondant à la séquence des touches menant de la racine de l'arbre à ce noeud.

Par exemple, l'arbre que l'on obtient pour le petit dictionnaire d'informatique composé des mots {hd, if, in, get, to, void, unit} est le suivant : 

                        {}
                       /  \
		     4/    \8
		     /      \
		   {}        {}
		  /  \        \
		6/    \3       \6
		/      \        \
	      {in}   {if,hd}    {to}
	                |        |
			|8       |4
			|        |
		      {get}     { }
		               /   \
			     3/     \8
			     /       \
			  {void}    {unit}
Pour représenter un tel arbre digital, on se donne le type Caml suivant : 
type trie = { words : string list ; branches : (int * trie) list }
i.e. chaque noeud de l'arbre est un enregistrement où le champ words contient la liste des mots correspondant à ce noeud et où le champ branches est une liste de paires associant des arbres digitaux à des entiers (on appelle précisément cela une liste d'association).
  1. Définir la valeur empty : trie correspondant au dictionnaire vide.

  2. Écrire une fonction find : trie -> int list -> string list renvoyant la liste des mots stockée dans le noeud désigné par la liste d'entiers passée en argument. (On pourra se servir de la fonction List.assoc de la bibliothèque Caml.)

  3. Écrire une fonction add : trie -> int list -> string -> trie ajoutant un mot dans le dictionnaire, la liste d'entiers correspondant au mot étant passée en argument. On pourra commencer par écrire une fonction 
    change_assoc : 'a -> 'b -> ('a * 'b) list -> ('a * 'b) list
    qui modifie (ou étend) une liste d'association.

  4. Écrire une fonction key : char -> int qui associe aux lettres minuscules de l'alphabet le chiffre correspondant sur le clavier d'un téléphone portable. En déduire une fonction intlist_of_string : string -> int list qui convertit un mot en la liste d'entiers correspondant à sa saisie sur le clavier du téléphone, puis une fonction add_word : trie -> string -> trie ajoutant un mot dans le dictionnaire.

  5. Construire le dictionnaire t correspondant à la liste de mots suivante : 
    let dict = [
  "lex"; "key"; "void" ; "caml" ; "unix" ; "for" ; "while" ; "done" ;
  "let" ; "fold"; "val"; "exn" ; "rec" ; "else" ; "then" ; "type" ;
  "try" ; "with" ; "to"; "find" ; "do" ; "in" ; "if" ; "hd" ; "tl" ;
  "iter" ; "map" ; "get"; "copy" ; "and"; "as" ; "begin" ; "class" ;
  "downto" ; "end" ; "exception" ; "false" ; "fun" ; "function" ;
  "match" ; "mod" ; "mutable" ; "open" ; "or" ; "true" ; "when" ;
  "load" ; "mem" ; "length" ; "bash" ; "unit" ; "site"; "php"; "sql";
  "ssh"; "spam"; "su"; "qt"; "root"; "bsd"; "boot"; "caml"; "bash";
  "ocaml"; "kde"; "gtk" ; "gcc"
]
    (On pourra utiliser pour cela la fonction de bibliothèque List.fold_left.)

    Tester avec le code suivant : 

    let () = assert (find t [2;2;6;5] = ["caml"])
let () = assert (let l = find t [4;3] in l = ["hd"; "if"] || l = ["if"; "hd"])
let () = assert (find t [4;3;8]   = ["get"])
let () = assert (find t [8;6;4;3] = ["void"])
let () = assert (find t [8;6;4;8] = ["unit"])

  6. Écrire une fonction remove_word : trie -> string -> trie permettant de supprimer un mot du dictionnaire.

    Tester avec le code suivant : 

    let t = remove_word t "caml"
let () = assert (find t [2;2;6;5] = [])
let () = assert (let l = find t [4;3] in l = ["hd"; "if"] || l = ["if"; "hd"])
let () = assert (find t [4;3;8]   = ["get"])
solution

3. Compression d'images

Un programme à trous quad.ml est fourni. Il suffit de le récupérer et de le modifier.

Le programme utilise la bibliothèque Graphics. Pour le compiler, il faut donc lier cette bibliothèque, à savoir : 
% ocamlc -o quad graphics.cma quad.ml
ou encore avec le compilateur natif : 
% ocamlopt -o quad graphics.cmxa quad.ml
Ceci produira l'exécutable quad. Cet exécutable dessine des images, puis s'arrête. L'affichage des images est contrôlé à l'aide des touches du clavier. À tout moment la touche « q » (avec le curseur de la souris dans la fenêtre graphique) permet de passer à la question suivante.

Les quadtrees

On présente ici une méthode originale de représentation d'images sous forme d'arbres. Cette représentation donne une méthode de compression plus ou moins efficace et facilite certaines opérations sur les images.

Pour simplifier, on suppose les images carrées, de côté 2n, et en noir et blanc. L'idée est la suivante : une image toute blanche ou toute noire se représente par sa couleur, tandis qu'une image composite se divise naturellement en quatre images carrées.

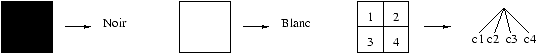
Selon ce schéma, les images sont représentées par des arbres du type suivant :

type couleur = Blanc | Noir

type arbre = Feuille of couleur | Noeud of arbre * arbre * arbre * arbre
On manipulera aussi des images bitmap, représentées par des matrices de couleurs que l'on supposera toujours de côté 2n par la suite. 

type image = couleur array array (* matrice de taille 2n *)

Échauffement

Écrire une fonction compte_feuilles qui prend un arbre en argument et renvoie le nombre de feuilles de cet arbre. Une fonction compte_feuilles grossièrement fausse est présente dans le squelette quad.ml ; à vous de la remplacer par la bonne.

Diverses conversions

Dessin de l'image

Nous pourrions inverser la fonction précédente. Mais il revient quasiment au même de dessiner l'image encodée par un arbre dans la fenêtre graphique.

Écrire donc une fonction dessine_arbre qui prend un entier k = 2n en argument et un arbre a, et qui dessine l'image encodée par a dans la fenêtre graphique opportunément taillée en k × k. Vous aurez certainement besoin de la fonction Graphics.fill_rect qui colorie un rectangle dans la couleur courante (ici le noir).

Les fonctions de test de quad.ml se chargent de la mise en place de la fenêtre et des appels à image_vers_arbre et à dessine_arbre. Normalement, vous deviez obtenir ce dessin :

(Si vous obtenez une isométrie quelconque de ce dessin, tranquilisez-vous et continuez.)

Arbre d'une image bitmap

Écrire une fonction image_vers_arbre qui prend un entier k et une image de côté k, et qui rend l'arbre représentant cette image. En Caml, étant donnée une matrice m, on accède à mi,j par m.(i).(j) (car en Caml une matrice est en fait un tableau de tableaux, ces derniers étant ici conventionnellement les lignes). Vous aurez peut-être besoin de consulter la documentation du module Array.

Transformations de l'arbre

Écrire les fonctions inverse, rotate et antirotate qui prennent toutes un arbre a représentant une image i en argument et renvoient un arbre représentant l'image inversée de i (blanc et noir échangés), i tournée d'un quart de tour vers la gauche, et i tournée d'un quart de tour vers la droite.

Le squelette permet de tester ces trois fonctions. Ainsi, la séquence de touches «n, i, p » devrait normalement donner ces images successivement :

  -- n -->    -- i -->    -- p -->  

On sort du test en appuyant sur la touche q.

Une fractale

Écrire une fonction fractale : int -> arbre qui prend un entier n en argument et construit l'arbre correspondant à n itérations du processus dont on montre ici les trois premières applications.

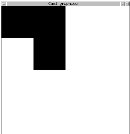
  -- n -->    -- n -->    -- n -->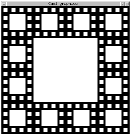  

(Il convient ici de bien regarder la première itération pour comprendre le processus.)

Le code fourni permet d'avancer dans les itérations avec la touche n et de reculer avec la touche p. On sort du test en appuyant sur la touche q.

Sauvegarde des images compressées

Dans le but de sauvegarder les images dans des fichiers, on se pose le problème de transformer le type arbre en une liste de 0 et de 1, ainsi que le problème réciproque.

On note code(a) la liste de 0 et de 1 représentant un arbre a. On choisit le codage suivant :

code(Feuille Blanc) = 00
code(Feuille Noir) = 01
code(Noeud (a1,a2,a3,a4)) = 1 code(a1) code(a2) code(a3) code(a4)

Pour simplifier on va procéder en deux temps : d'abord le codage (et décodage) de l'arbre en liste de bits ; puis l'écriture (et lecture) des bits dans un fichier.

Des arbres vers les listes, et retour

On se donne d'abord un type pour les bits (zéro ou un). 
type bit = Zero | Un
Écrire une fonction arbre_vers_liste de type arbre -> bit list qui transforme un arbre en une liste de 0 et de 1 selon le codage ci-dessus. Cette fonction ressemble furieusement à l'affichage d'un arbre sous forme préfixe.

Écrire la fonction réciproque liste_vers_arbre de type bit list -> arbre, qui transforme une liste de bits en l'arbre correspondant. Cette fonction ressemble à l'analyse syntaxique d'une expresssion donnée sous forme préfixe, le codage choisi évitant les ambiguïtés.

Écriture et lecture

Terminer la question, c'est-à-dire écrire les fonctions ecrire_arbre de type string -> arbre -> unit et lire_arbre de type string -> arbre, qui respectivement sauvegarde un arbre dans un fichier dont le nom est passé en argument, et lit l'arbre contenu dans un fichier.

On cherche bien évidemment à produire les fichiers les plus petits possible. L'idée est simple et classique, les fichiers étant des suites de caractères qui sont aussi des entiers sur 8 bits. On va donc grouper les bits par paquets de 8 dans des entiers normaux, convertir ces entiers en caractères (voir Char.chr), puis écrire les caractères dans le fichier.

Les fonctions sur les fichiers sont regroupées dans le module Pervasives (ouvert par défaut, ainsi on n'est pas obligé de faire précéder ces fonctions de Pervasives.). On portera un intérêt tout particulier à l'ouverture (open_out et open_in) et à la fermeture (close_out et close_in) d'un fichier, ainsi qu'à l'écriture et à la lecture d'un caractère (output_char et input_char).

Le squelette fourni contient un test (sauver et relire une des fractales de la question précédente), mais vous pouvez aussi lire cette image.
solution
retour à la page du cours